Shorting Paired ETFs

The Strategy No One Dares Risk

I believe that the best investment is one that leverages mispricing. And I'm not alone, as hedge fund managers often base their own strategies around buying undervalued and selling overvalued investment instruments. Some mispricing phenomena are due to miscorrelations between certain instruments. Some traders have found that leveraged, paired ETFs (one bullish, one bearish), such as (FAS) and (FAZ) or (VXX) and (XIV), are not perfectly correlated; shorting both the ETFs simultaneously proves to be profitable. Some traders, such as Seeking Alpha contributor David Oldenburg have even followed through with the trade, coming out with profit. Unfortunately, this trading strategy presents several problems, which is why few risk it.

Problem 1: Unlimited Risk

Any look at paired ETFs will show you that should you have shorted them both, you would come out with a profit in most cases. But the opportunity for a black swan event in which one of the two ETFs experiences a spike exposes you to unlimited risk. And the possibility for that is twofold: A market crash will spike the inverse ETF; a market surge will spike the bullish ETF. You're exposing yourself to two unlimited risks, for a limited gain.

Thus, we must solve this problem by hedging against this risk. Or better yet, turning the unlimited risk into a reasonable, manageable risk.

Problem 2: Time Decay Too Slow

The time decay (the money that comes over time from the miscorrelation between the two ETFs) that is ultimately our profit source of this trading strategy is rather slow. Even a short spike in the more expensive of the two ETFs could quickly wipe out a month's worth of time decay profit. I'll illustrate this by example. If the expensive ETF, let's say it's trading at $100, jumps by 10% (not uncommon for a leveraged ETF), you've just lost $10. Now, if the inverse is trading at $50, theoretically, it should also drop 10%, giving you a profit of $5. Overall, you are out $5 per share from a temporal spike. If you haven't made more than $5 from the time decay, you'd entered into a losing trade.

The solution to this is to find a way to speed up the time decay so that these temporal spikes don't affect our earnings too much.

Problem 3: Shorting Stock Isn't Free

Unlike buying stock on a one-time commission basis, shorting stock carries a borrow rate. As shorting stock is essentially equivalent to taking out a loan, you'll need to ensure that the money you gain from shorting paired ETFs over time exceeds the borrow rate. This is not an easy task, as the borrow rate changes every day and across brokerages.

The solution is to avoid this borrow rate so that you can reap the rewards of time decay without having to fight against the time decay of the loan.

How Is My Strategy Different?

When I reflected on all these problems, the solution became immediately clear to me. I primarily trade options, and options can solve all of the above problems. What I posit is a strategy that simulates shorting two ETFs by selling call options on the ETFs.

The Options Solution to the Unlimited Risk Problem

Selling a call option also exposes you to unlimited risk. But buy buying a call option of a higher strike price, you limit your risk. There is flexibility in this. Not only can you limit your risk, but you can specifically define your maximum risk. This strategy, the bearish credit spread, presents a myriad of "insurance policies" against a black swan event. For example, if you're not willing to risk more than $100 loss per contract, you can buy a call option with a strike price $1 above the sold call option. If you're more risk-seeking and want more profit from the trade, you can go way above that, perhaps $10 higher; this way, you have insurance but it doesn't eat too much into your profit from the sold call option.

The Options Solution to the Slow Time Decay

Playing the dual shorting of paired ETFs pays off over time. To speed up that process, selling call options innately helps out, as they themselves have time decay. Thus, you are profiting from three sources of time decay: that on the mismatch of the prices in the ETFs and that on the call options on the ETFs (one for each ETF).

The Options Solution to the Borrow Rate

To sell a call option, you only need provide margin. No loan required. And when you run a credit spread, you can even control the amount of margin you need to put up. Naked calls obviously require the most margin. But tight credit spreads require little margin.

The Complexity Hike

This trading strategy is necessarily more complex than merely shorting paired ETFs. You will need to decide on four strike prices and an expiration date. And I cannot give you an optimal set of these choices because every investor's risk tolerance differs. However, I can outline some guidelines:

The sold calls' strike prices should be OTM if you have low risk tolerance.

You can consider ITM call options if you're not afraid of being exercised.

The bought calls' strike prices should match how much you're willing to risk should a black swan event occur. Every $1 in strike price exposes you to $100 more potential risk, minus what you got for selling the option trade.

Longer expiration dates expose you to higher risks of being exercised.

Shorter expiration dates bring in less profit but have higher theta.

An Example

While I would love to backtest this strategy, I do not have access to historical options prices, precluding the potential for a legitimate backtest. Thus, I will merely present an example of a trade I might make today if I were to employ this strategy. While I'd love to do this on the VXX and XIV, the XIV doesn't trade options. Hence, I will go with my second choice: FAS and FAZ.

Here are my trades:

(click to enlarge)

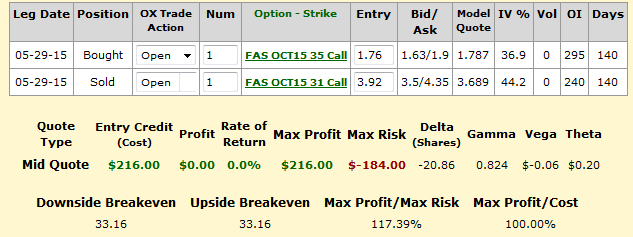
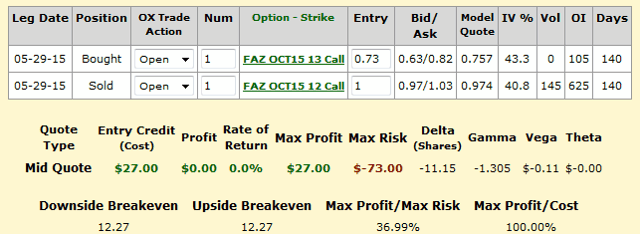
The FAS trade is ITM while the FAZ trade is OTM. I decided on these trades by analyzing various ratios and the Greeks via Platinum Options. This might not be the optimal choice - and please tell me what you would change in the comments section below - but for me, it seems like a reasonable trade.

For these trades, I would be selling the credit spreads at a ratio of 5-to-1; that is, 5 FAZ credit spreads and one FAS credit spread. This maximizes my risk to $500 per trade, minus what I gained for the trade. For FAS and FAZ respectively, the max risks are $184 and $365. The max profit is $351 per trade (this occurs if both FAS is below 31 in October and FAZ is below 12 in October). Because it is theoretically impossible for both FAS and FAZ to rise, my max risk seems to be under the max profit of the trade: Assume a 50/50 chance of one spiking to get the averaged risk: (184+365)/2=274.5. This gives a reward-to-risk ratio of about 1.28. Compare this risk to shorting both ETFs; that is, infinite risk.

In addition, the long expiration date gives me the ability to close the position prior to expiration should I see an opportunity to buy back the options at a cheap price, such as if FAS falls below 31 while FAZ is still below 12.

In October, I will revisit this trade via another article to recap on how it went.